TA百人计划 图形 1.2.3 MVP矩阵运算
不同空间的坐标转换部分的内容。p矩阵推导不知道对不对捏
笔记
为什么学矩阵变换
- 将3D物体转换到2D平面
- 掌握矩阵变换过程才能运用矩阵变换达到自己想要的目的
MVP矩阵是什么
MVP矩阵表示的是模型(Model)、观察(View)、投影(Projection)三个矩阵。
起始情况获得的物体坐标位于局部空间(Local Space)下,将它的坐标称为局部坐标(Local Coordinate)。
之后需要依次转换到世界坐标(World Coordinate)、观察坐标(View Coordinate)、裁剪坐标(Clip Coordinate),最后转为屏幕坐标(Screen Coordinate)。
M矩阵
将坐标从模型空间转换到世界空间
模型空间:以模型自身为中心的坐标空间
世界空间:世界为中心的坐标空间
操作矩阵
$M=\left[\begin{matrix}
1&0&0&tx\newline
0&1&0&ty\newline
0&0&1&tz\newline
0&0&0&1\newline
\end{matrix}\right]
\left[\begin{matrix}
cos\theta &0&sin\theta&0\newline
0&1&0&0\newline
-sin\theta&0&cos\theta&0\newline
0&0&0&1\newline
\end{matrix}\right]
\left[\begin{matrix}
kx&0&0&0\newline
0&ky&0&0\newline
0&0&kz&0\newline
0&0&0&1\newline
\end{matrix}\right]
$
从右到左进行计算
- 进行缩放操作
- 进行旋转操作
- 进行平移操作
V矩阵
将坐标从世界空间转换到摄像机为中心的观察空间
相当于把摄像头从它自己的局部空间转换到世界空间操作的逆操作。因为摄像头没有大小,本身就是观察空间的原点,不需要缩放。
操作矩阵
$M=\left[\begin{matrix}
1&0&0&0\newline
0&cos\theta&-sin\theta&0\newline
0&sin\theta&cos\theta&0\newline
0&0&0&1\newline
\end{matrix}\right]
\left[\begin{matrix}
1&0&0&tx\newline
0&1&0&ty\newline
0&0&1&tz\newline
0&0&0&1\newline
\end{matrix}\right]
$
unity下使用的是左手坐标系,但是观察空间用的右手坐标系。所以z分量需要取反。所以在unity中应该这样
$M=\left[\begin{matrix}
1 & 0 & 0 & 0 \newline
0 & 1 & 0 & 0 \newline
0 & 0 & -1&0 \newline
0 & 0 & 0 & 1
\end{matrix}\right]
\left[\begin{matrix}
1&0&0&0\newline
0&cos\theta&-sin\theta&0\newline
0&sin\theta&cos\theta&0\newline
0&0&0&1\newline
\end{matrix}\right]
\left[\begin{matrix}
1&0&0&tx\newline
0&1&0&ty\newline
0&0&1&tz\newline
0&0&0&1\newline
\end{matrix}\right]
$
P矩阵
这东西看视频没看懂。入门精要讲的要详细易懂些。https://candycat1992.github.io/unity_shaders_book/unity_shaders_book_chapter_4.pdf
将观察空间下的坐标转换到其次裁剪空间下。对x,y,z分量进行缩放。并没有真的做投影操作。
变换后的矩阵里w分量正好具有特殊意义,可以用来裁剪视锥体外的顶点。
只要满足$\begin{cases} -w \leq x \leq w \newline -w \leq y \leq w \newline -w \leq z \leq w\end{cases}$的顶点就能保留下来
透视投影
满足近大远小的透视规则。视锥体是个平截头四棱锥。
正交投影
没有透视关系。视锥体是个长方体。
操作矩阵
透视投影:
$P=\left[\begin{matrix}
\frac{cot\frac{FOV}{2}}{Aspect} & 0 & 0 & 0 \newline
0 & cot\frac{FOV}{2} & 0 & 0 \newline
0 & 0 & \frac{Far+Near}{Far-Near} & -\frac{2\cdot Near\cdot Far}{Far-Near} \newline
0 & 0 & -1 & 0
\end{matrix}\right]$
正交投影:
$P=\left[\begin{matrix}
\frac{1}{Aspect\cdot Size} & 0 & 0 & 0 \newline
0 & \frac{1}{Size} & 0 & 0 \newline
0 & 0 & -\frac{2}{Far-Near} & -\frac{Far+Near}{Far-Near} \newline
0 & 0 & 0 & 1
\end{matrix}\right]$
各个参数含义参考精要PDF84页
应用
- 世界空间:顶点坐标乘以M矩阵转换为世界空间坐标,取zx作为uv进行采样可以获得不规则平面的Tilling。
- 视觉空间:顶点坐标转换到视觉空间下,根据远近距离显隐变换。
光栅化补充
作业
模型空间、世界空间、视野空间的区别
模型空间
每个模型独立的空间坐标系。以模型中心为原点。
世界空间
以世界中心为原点,整个世界独一无二的坐标系。
视野空间
以摄像机为原点,每个摄像机各自拥有各自的视野空间。
推导p矩阵
这部分参考的GAMES101
正交投影
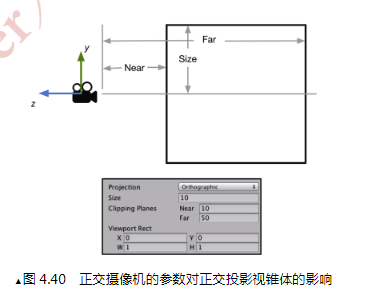
基本思想是。先把视锥体的中心点平移到坐标原点,然后缩放到每个分量[-1,1]范围内的一个规范视域体。
按照入门精要这里的插图描述,视锥体中心点为$\left[0, 0, -\frac{Far-Near}{2}\right]^T$
平移矩阵$M_{Trans} = \left[\begin{matrix}
1 & 0 & 0 & 0 \newline
0 & 1 & 0 & 0 \newline
0 & 0 & 1 & -\frac{Far-Near}{2} \newline
0 & 0 & 0 & 1
\end{matrix}\right]$
z轴缩放比例$\frac{2}{Far-Near}$, y轴缩放比例$\frac{1}{Size}$ ,x轴缩放比例$\frac{1}{Aspect\cdot Size}$
缩放矩阵$M_{Scale}=\left[\begin{matrix}
\frac{1}{Aspect\cdot Size} & 0 & 0 & 0 \newline
0 & \frac{1}{Size} & 0 & 0 \newline
0 & 0 & \frac{2}{Far-Near} & 0 \newline
0 & 0 & 0 & 1
\end{matrix}\right]$
正交投影矩阵$M_{Ortho}=M_{Scale}\times M_{Trans} = \left[\begin{matrix}
\frac{1}{Aspect\cdot Size} & 0 & 0 & 0 \newline
0 & \frac{1}{Size} & 0 & 0 \newline
0 & 0 & \frac{2}{Far-Near} & \frac{Near-Far}{Far-Near} \newline
0 & 0 & 0 & 1
\end{matrix}\right]$
透视投影
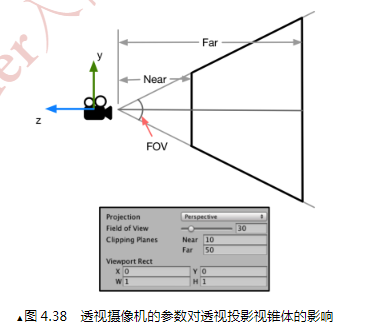
基本思想:把视锥体变换为正交投影的长方体形式,再以正交投影方式计算。
把任意平面变换到近平面同一尺寸。使视锥体成长方体。
任意一点(x,y,z)的坐标变换后将变成
$\left[\begin{matrix}
\frac{Near}{z} \cdot x & \frac{Near}{z} \cdot y & Unknown& 1
\end{matrix}\right]^T$。这里z的值并不是不变的!$z'=Near+Far-Near\cdot \frac{Far}{z}$,在Near到Far范围内实际上映射后的z值会更偏向于远平面。这里不关心具体情况用Unknown代替
点乘上非0系数后仍然是同一个点。这里z值一定是大于0的,所以可以乘上一个z变成$\left[\begin{matrix}
Near \cdot x & Near \cdot y & Unknown& z
\end{matrix}\right]^T$。写成矩阵形式
$M_{Persp\rightarrow Ortho}=\left[\begin{matrix}
Near & 0 & 0 & 0 \newline
0 & Near & 0 & 0 \newline
? & ? & ? & ? \newline
0 & 0 & 1 & 0
\end{matrix}\right]$
取点在近平面的情况,那么变换前后坐标不变。
$M_{Persp\rightarrow Ortho}\cdot \left[\begin{matrix}x\newline y\newline\ Near\newline 1 \end{matrix}\right]=\left[\begin{matrix}Near\cdot x\newline Near\cdot y\newline\ Near^2\newline Near \end{matrix}\right]$
只考虑第三行,结果已经跟x、y没关系了,所以前两个数为0。矩阵为
$M_{Persp\rightarrow Ortho}=\left[\begin{matrix}
Near & 0 & 0 & 0 \newline
0 & Near & 0 & 0 \newline
0 & 0 & ? & ? \newline
0 & 0 & 1 & 0
\end{matrix}\right]$
同时。取点在远平面的情况。z值也是确定的,并且取远平面的中心点代入,x和y的值都取0。
$M_{Persp\rightarrow Ortho}\cdot \left[\begin{matrix}0\newline 0\newline\ Far\newline 1 \end{matrix}\right]=\left[\begin{matrix}0\newline 0\newline\ Far^2\newline Far \end{matrix}\right]$
设第三行未知的两个数分别为a和b.
计算$\begin{cases}a\cdot Near+b=Near^2\newline
a\cdot Far+b=Far^2\end{cases}$得到$a=Near+Far,b=-Near\cdot Far$
最终透视投影到正交投影变换的矩阵$M_{Persp\rightarrow Ortho}=\left[\begin{matrix}
Near & 0 & 0 & 0 \newline
0 & Near & 0 & 0 \newline
0 & 0 & Near+Far & -Near\cdot Far \newline
0 & 0 & 1 & 0
\end{matrix}\right]$
最后透视投影的矩阵$M_{Persp}=M_{Ortho}\cdot M_{Persp\rightarrow Ortho}=
\left[\begin{matrix}
\frac{1}{Aspect\cdot Size} & 0 & 0 & 0 \newline
0 & \frac{1}{Size} & 0 & 0 \newline
0 & 0 & \frac{2}{Far-Near} & \frac{Near-Far}{Far-Near} \newline
0 & 0 & 0 & 1
\end{matrix}\right]
\left[\begin{matrix}
Near & 0 & 0 & 0 \newline
0 & Near & 0 & 0 \newline
0 & 0 & Near+Far & -Near\cdot Far \newline
0 & 0 & 1 & 0
\end{matrix}\right]$
$=\left[\begin{matrix}
\frac{Near}{Aspect\cdot Size} & 0 & 0 & 0\newline
0 & \frac{Near}{Size} & 0 & 0 \newline
0 & 0 & \frac{3Near+Far}{Far-Near} & -\frac{2Far\cdot Near}{Far-Near}\newline
0 & 0 & 1 & 0
\end{matrix}\right]
$
这里Size为近平面的高$h=tan\frac{FOV}{2}\cdot Near$。代入获得。
$\left[\begin{matrix}
\frac{cot\frac{FOV}{2}}{Aspect} & 0 & 0 & 0 \newline
0 & cot\frac{FOV}{2} & 0 & 0 \newline
0 & 0 & \frac{3Near+Far}{Far-Near} & -\frac{2Far\cdot Near}{Far-Near}\newline
0 & 0 & 1 & 0
\end{matrix}\right]$
为什么两个矩阵算出来的z跟精要里给出来的不一样捏?总觉得这插图跟实际的z方向是相反的。